Effect of popular items

事實上我們還需要考慮一個與 co-occurrence matrix 相關的重要問題

就是 normalization 為什麼這麼說呢？

我們先來看當一個商品需求量極大時會如何，同樣以尿布為例，我們假設它需求量極大

同樣的當我購買了嬰兒相關商品後，我透過這個矩陣，只會得到尿布，因此我們需要更個性化的推薦

像是很多人買尿布，並不代表我買了嬰兒玩具也想買尿布，那該怎麼作到呢？

我們得克服流行商品推薦力過強的因素

Normalizing co-occurrence matrices and leveraging purchase histories

為了要處理這個問題，我們必須將 co-occurrence matrix 做 normalization

這與 clustering 和 similarity module 非常像

我們那時候在說 tf-idf 時曾遇到出現頻率極高的詞會覆蓋覆蓋掉我們關心的詞

在那個時候我們就採取了 normalization，同理我們當然可以一樣拿來處理流行商品問題

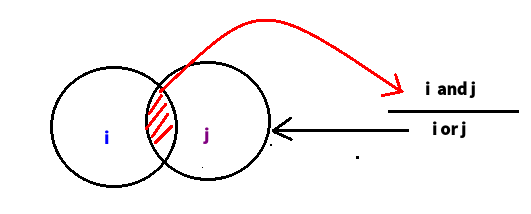
統計同時購買i與j的人(i and j)並除上 (i or j)

我們可以直接透過這張圖為例，這樣就可以完成我們的 normalization 了

但是其實這種方法還是有一些侷限，其中一個問題是你只考慮目前的狀態，再跟我推薦時你並沒有將購物的歷史紀錄考慮進去，因此我們可以做些調整，將歷史紀錄加進來，該怎麼做呢？

一種簡單的方式是，每次我幫商品打分數加上權重係數，所有歷史紀錄都要加上

#User bought items {diapers, milk}
Score( user , baby wipes) = ½ (Sbaby wipes, diapers + Sbaby wipes, milk) 

Sort Score( user , j ) and find item j with highest similarity 

比如我買了尿布與牛奶，接下來跟我推薦，我將瀏覽整個推薦並且打分數

假設我現在需要嬰兒溼紙巾，此時就會算出推薦嬰兒濕紙巾的權重係數，計算方式同樣的就是找到尿布的陣列，並且看同時買嬰兒濕紙巾與尿布的值，並且同時找到買牛奶又買嬰兒濕紙巾的值

由這兩個值的平均值來得到購買的可能性，當然不僅如此，我們甚至可以進一步將時間做為變數

越是靠近最近買的商品其權值越大，最終我們就是將加權平均數排列，挑出最高分來推薦

跟之前很像，不過多了歷史紀錄的權重係數

這個方法仍舊有些缺陷，比如購物發生的時間和使用者的特徵(性別、年紀...)

它僅僅是考慮了 co-occurrence matrix

另一個問題是 Cold start 問題，這個問題在諸多領域都會碰到

當我們要考慮一個新商品或使用者時，此時我們就會碰到 Cold start

我們沒有使用者過去購買歷史，新的商品也沒有跟其他商品同時被購買的次數

The matrix completion task

截至目前為止，我們討論的 co-occurence 方法中，並沒有從我作為一名使用者各方面或商品所具備的特徵

反而從購買量與購物歷史進行

因此我們要問，是不是有一個方法關於我是誰與依照商品訊息，如同我們在分類的方法中所討論的，我們將有一些使用者與產品的特徵，從這裡我們想從資料中學習特徵

另外我們還想考慮使用者與商品間的交互作用，就像是 co-occurence 一樣

接下來的討論背景是用在一個電影推薦系統

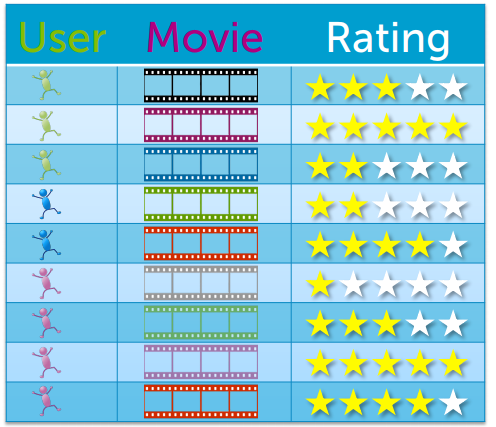
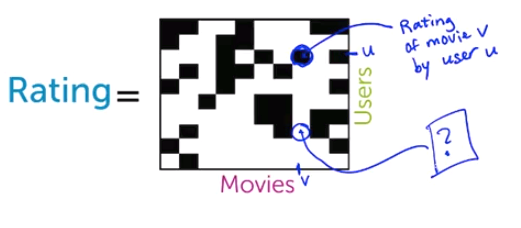
在這個應用中，我們擁有的資料就是這個大表格，表格中我們收集了大量使用者資訊及他們看過得電影跟電影的評價

想像一下有三個用戶分別上線看了某些電影並留下評論

我們將可以得到"使用者、電影、評論"這個表格，而每個使用者只看了當中幾部電影

接著我們將這個資料表轉成一個巨大的使用者對電影評論的矩陣，這個矩陣非常稀疏，原因是這裡的使用者雖多，但是看過不過是某幾部電影而已

• 黑色表示用戶x對電影y的評價(rating(x,y))
• 白色方塊代表著一個未知的問號(至少這部電影還沒得到評價)，這邊要注意的是沒有評價不代表不喜歡
• 我們目標是填寫這些未知的白色方塊
• 接下來要使用到的是你對其他電影評價，以及其他用戶對這部電影的評價
• 我們將運用這些黑色來預測這些白色
• 我們使用了你以及其他使用者的歷史評價來預測，其他使用者對於尚未觀看的電影評價

Reference:

• Machine Learning Foundations: A Case Study Approach 華盛頓大學在 coursera 上的公開課程，為本筆記追蹤的主要素材
• 課程投影片